What is a Netmask (or Genmask)? And why is understanding it so important when it comes to network routing?
What exactly is a netmask? An industry-standard term, netmask is an abbreviation for "sub-network mask." Genmask is a term unique to iproute and purportedly was coined as a reference to the "general netmask" of a route. To be clear, "netmask" and "genmask" are the same thing.
Table of Contents
Routers and Routes
Routes are instructions, but they are easier to fathom if you think of them as filters. Within a route, there are two filtration layers: an IPv4 host address and a netmask. The netmask filter is superimposed over a single destination host address. The netmask is used to amplify the scope of the route. The result defines a range of IPv4 host addresses.
Why? Without the netmask concept, routers would be slow and require vast amounts of resources to perform their function. It would also be exceptionally tedious to manage them. There are over 4.2 billion routable IPv4 addresses. Can you imagine having to create an independent route for every one of those addresses? It's just not practical. Together, an IPv4 address and netmask are combined to create an address range out of that 4+ billion pile of addresses.
If you're familiar with photography, you can liken the process to a variable focus camera lens. Imagine a single IPv4 address is your base - a fixed focal lens - and the netmask is a variable zoom lens mounted to the base lens. The variable lens (netmask) allows the breadth of your focus (address range) to be very broad, very narrow, or somewhere in between. Just as a variable focus lens may zoom in to a specific point or zoom out to capture a wide view, the netmask controls the scope of a route's address range. It allows the router to narrow its focus between one (1) and ALL possible IPv4 addresses; from fine to coarse focusing per se.
4x8=32
Computers distill all communications down to binary signals of 0 and 1. IP addresses are no exception. As humans, we are used to working with IPv4 addresses in a 10-base numeral format, but that is simply for our convenience. In reality those are not the real IP addresses. Each of those 3-digit, 10-base values we're accustomed to are converted to 8-bit binary numbers that computers understand. Four (4) of those 8-bit numbers are combined, resulting in an aggregate 32-bit string (4x8=32) which represents an individual IPv4 host address on the network.
You may have noticed every number in an IPv4 address falls into a range between 0 and 255.
An 8-bit number in the binary number system has a range of 0-255 when converted to a 10-base (decimal) value. The bits in an 8-bit number are powers of 2. Each consecutive bit is 2-to-the-power of its position. For example, the 4th bit is equivalent in value to 2^4 or 16. The bits are accretive. If both the 3rd and 4th bits are set (equal to 1), you would have the equivalent of 8+16 or 24 (2^3 + 2^4 = 8 + 16 = 24). If all the bits are set, the value is 255. If none are set, the value is 0 (zero). This chart illustrates how an 8-bit group of binary bits equates to 10-base integer values. By adding together the "on" binary bits, a 10-base integer range between 0-255 is attained.
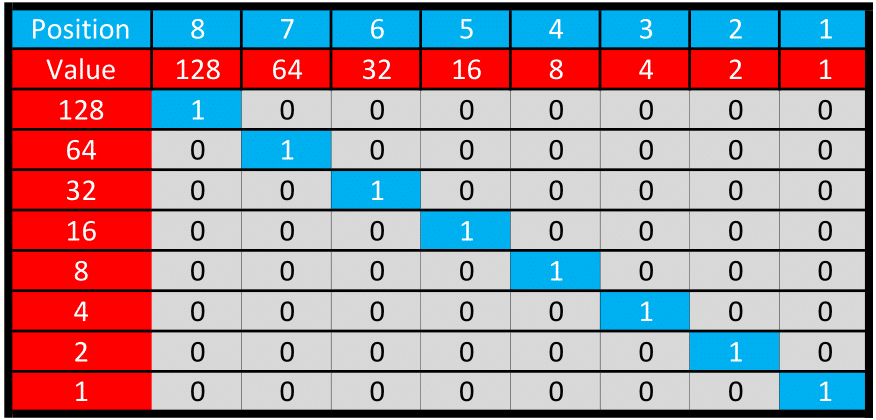
Figure: 8-bit Illustration (Big-endian format)
Now that we've reviewed the 8-bit values that make up IPv4 host addresses and explained how they are combined to form a 32-bit string, let's shift the focus to routers and routes. Did you know that to a router, an IPv4 network address is actually 64-bits in length? How is that possible?
8x8=64
When you type an IPv4 network address into a browser, you are either typing it in the format aaa.bbb.ccc.ddd (the host address on the network), or the host's Fully Qualified Domain Name (FQDN; e.g. abc.com), which is then converted to a host address by a Domain Name Server (DNS).1 Either way, as described above, those IPv4 addresses we are accustomed to are in fact a set of four (4) 8-bit numbers, and when combined they represent a single 32-bit string. So, I mentioned routers and routes use a 64-bit string. Where does the other 32-bits come from?
Routers use 64-bits of address data to quantify routes. When it comes to IPv4 addresses, it's actually 2x 32-bit strings and not a single 64-bit string. You can probably see where this is going. That 32-bit netmask is often expressed as a group of 4x 8-bit values.
If you spread out an IPv4 destination address and a route's corresponding netmask, you'll see we have eight (8) numbers in a range from 0-255. That's 256 possible numbers in each slot or 2^8 possible values for each of the eight (8) numbers (and thus each can be represented in binary form by an 8-bit number).
0.0.0.0 | 255.255.255.255
The router takes that human-readable format and converts it into eight (8) 8-bit numbers, which can also be grouped into two sets of 32-bit numbers, which is how it views the IPv4 host address and netmask respectively. 8 numbers x 8 bits = 64 bits.
00000000.00000000.00000000.00000000 | 11111111.11111111.11111111.11111111
As you can see, the 64-bit values used by routers to represent IPv4 addresses are a conglomeration of the 32-bit IPv4 host address (also known as the Routing Prefix), and the 32-bit sub-net mask.
IPv6 addresses are natively 64-bits. IPv6 host addresses do not use netmasks.
Netmask Re-cap
The sub-net mask is commonly referred to as the netmask for short. The netmask describes the size of a sub-network, and is applied to the host address in the routing prefix. When represented in 10-base form, the combination of IPv4 address and netmask together form an octet (a group of 8 numbers) - each consisting of an 8-bit value - for a total of 8x 8-bits or 64-bits total. Each individual number in the set is sometimes colloquially referred to as an octet of the IPv4 address, though the term is technically inaccurate. A netmask may also be represented using a form known as slash notation.
Here's how it all works.
Subnets and Netmasks
Sub-netting is the process of dividing a network into smaller networks or segments. If you need a primer on sub-networks and netmasks, I suggest reading Routers, Routes, Subnets, and Netmasks before proceeding.
Slash Notation
Slash notation is a simplified representation of a route's netmask bits. It appears as "IPv4 address/xx" where "xx" is a whole number between 0-32. The number after the slash represents the number of bits which are "on" (set to 1) in the 32-bit netmask string. The slash notation may be any number between 0 and 32.
Most people find it easier to use as a shorthand method of assigning netmasks. However, if you are using tools such as the route command and/or certain legacy tools, such as netstat, the output of those tools is virtually always presented in a 10-base number format, thus requiring some ability to translate those figures to binary representations. Many online tools exist to assist with this process, as it is a common task for network administrators. A table of recommended online IPv4 conversion tools is provided at the end of this article.
Netmask bits "mask" the range of IPv4 addresses addressed by the route. The fewer the number of bits used in masking, the wider the net that is cast over a range of IPv4 addresses. Conversely, higher numbers (more bits set) narrow the focus. The use of slash notation numbers less than eight (8) is extremely rare as it begets filtering very large networks. Most corporate and local networks use netmask values of 24 or higher. The nuances are explained below in greater detail.
Valid Netmask Values
The world of netmasks is not quite as wide open and flexible as it might first seem. Only certain numbers are valid for netmasks. Viewed as a binary number, the left portion of the netmask begins with one or more one (1) or set bits. At some point, the bits flip to zeroes (0's). Viewed as a 32-bit string, netmask bits are always ones (1) on the left portion of the string and zeroes (0) on the right portion. You cannot have a one (1) bit to the right of any zero (0) bit. This concept can be confusing at first, and it is one reason why the slash notation method is often much easier to comprehend and keep track of correct netmask notation. Here are a couple of examples to illustrate.
This netmask is valid:
11111111.11111111.11111111.10000000
At 25 bits wide, it represents 255.255.255.128 or /25 in slash notation.
The netmask below is not valid. Do you see why? The one (1) bits to the right of the first zero (0) - when viewed from left to right - are not valid, because they are to the right of the last consecutive one (1) bit. As soon as a zero (0) appears when viewing from left-to-right, you cannot have more ones (1's) in the string.
11111111.11111111.11111111.10110010
The invalid example above would either generate an error and the route would be ignored, or the last 7 bits would be ignored and the netmask would be applied as /25 (honoring only the first 25 bits before the 1st zero).
As you can see, it's easier to conceptualize the netmask's function when viewing it from the perspective of binary digits instead of decimals. This is because when you look at them as binary numbers, their masking effect becomes obvious. Presented in binary form, a netmask is always going to look like one or more ones (1's) followed by one or more zeroes (0's). When the netmask is expressed with a slash and a single number, the format is aaa.bbb.ccc.ddd/xx, where xx represents the number of "on" bits in the netmask, and is an integer between 0 and 31. These "on" bits will always be at the beginning of the binary string that represents the netmask. For example, 192.168.10.10/14 has a slash notation netmask of "/14." A routing device would convert "14" to a 32-bit binary form netmask, which would look like this:
11111111.11111100.00000000.00000000
Notice there are... wait for it... 14 ones (1's) and all the bits after the 14th one (1) are zeroes (0). If you converted that binary value into a 10-base (decimal) octal value for the netmask, you'd get 255.252.0.0. Now, you can begin to see how the bits are converted into 10-base numbers and vice-versa. The IPv4 address range 192.168.10.10/255.252.0.0 is the same as 192.168.10.10/14.
Remember, it's all about the bits!
A netmask simply describes the size of a network segment (number of hosts referenced by a route). A router takes the combination of the IPv4 host address (routing prefix) and combines it with the netmask to create a range of IPv4 addresses. When a packet's destination falls within that range, it is further scrutinized to determine if it is the longest matching route for the current packet. If so, the route is selected and the current packet is dispatched via that route.
Network Masking Deep Dive
We've reviewed the netmask concept at a high level, and how routers use it to filter ranges of IPv4 host addresses by interacting with a single IPv4 host address. But, we have not discussed exactly how a route identifies the starting or lower boundary IPv4 address of a range, and how it identifies the ending or upper boundary IPv4 address in a range. This is obviously a critical point to understand if you're going to create sub-networks and routes. So, how does the IPv4 netmask concept work? How does it segment or partition a network?
Surprise! There is yet another logic layer you should become familiar with: the wildcard mask.
The Wildcard Mask
The wildcard mask or wildcard is a 32-bit inverse of the netmask.
What is the purpose of the wildcard? It's used to determine the upper boundary address of the range, using a two-step process. First, a logical NOT operation is applied to the netmask. Then, the wildcard value is added to the lower boundary via a logical OR operation, which produces the upper boundary address.
The wildcard also has a secondary function. It identifies the number of host addresses in the sub-network range. I know that sounds like the same definition as the netmask ("size" of the address range), but there is a subtle difference. The netmask is used to identify the host address at the top end (upper boundary) of the IPv4 address range of the route. The wildcard identifies the number of IPv4 host addresses within the boundary range of host addresses.
How Masks Work
Routers reference host addresses and netmasks in binary form. Masks are a logical method of comparing two values. Routes use masks to make comparisons between host addresses and target values. How do masks work? When masks are applied, logic operands come into play. Usually, AND, OR, and NOT.
The most common masking processes is the AND operand. The classic definition of a mask is logically ANDing a source value and a mask, resulting in only the bits matching the mask passing through. That's the gist of how a mask works, though exactly which operands are applied with a particular mask varies. The specifics of each masking process are explained in detail throughout this document in the relevant sections, but at a high level, the AND operand is the key to masking.
This table shows the types of masking operands used in each of the masking processes discussed in this article:
| Mask | Operand | Value1 | Value2 | Purpose |
|---|---|---|---|---|
| Netmask | AND | IPv4 Host Address | netmask | Define a sub-network |
| Wildcard | NOT | netmask | Inverse of the Netmask | |
| Lower IPv4 Range Boundary | AND | IPv4 host address | netmask | 1st IPv4 in sub-net |
| Upper IPv4 Range Boundary | OR | lower boundary | wildcard | Last IPv4 in sub-net |
A tutorial on logical bit operators is beyond the scope of this guide. I have to presume you are familiar with logic gates. If not, you should invest some time in learning about them because routers rely on bitwise operators.
Bitwise Functions
As humans, we tend to think of numbers in a 10-base format, but computers view them as binary or 2-base numbers. "Bitwise" is a term that refers to digital processes capable of acting at the level of individual bits or groups of bits. Routers are bitwise, and so are all their functions discussed in this article. Just in case you do need a little background primer, I'll briefly expound on the AND operator, using the netmask filtering concept to illustrate.
The Mighty AND
A route starts with an IPv4 host address, and the netmask is applied as a mask using a logical AND operation at the bit level. This has the effect of screening only the IPv4 addresses with bits that match the netmask, and creates a new result (referred to in this article as the lower boundary IPv4 address). Next, the current packet's destination host address is evaluated against this lower boundary filter. If the packet's IPv4 address is less than or equal to the lower boundary, it passes the mask, and the router continues processing the route's filters. If the destination address doesn't match, the router aborts this route and moves on to the next one in the routing table.
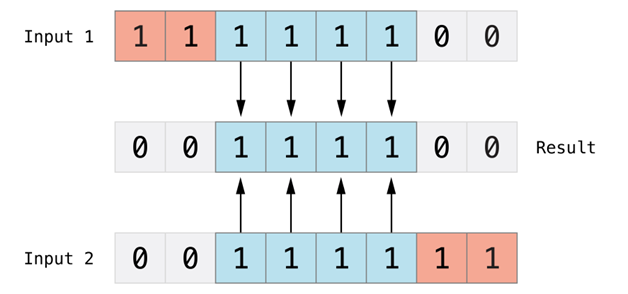
Figure: AND Bit Logic Illustration
When the router reaches the end of the router table, it moves on to the next table in the routing table database. This process is repeated for ALL routing tables. Only after all this screening has occurred does the router isolate the most specific route matching the packet, which is the route the packet will be sent out on.
Here's what an IPv4 address looks like to you versus a router:
| IPv4 Address | Netmask | What the Router Sees |
|---|---|---|
| 192.168.10.0 | 255.255.255.0 | 11000000.10101000.00001010.00000000 |
Netmask Examples
One of the best ways to fully digest all this information is to walk through some examples....
Example 1: The Power of Zero (Default Route)
There a few host addresses, gateways, and masks that are special for one reason or another. The most important is the default route. A "default" route (as its name implies) is where all traffic will be routed unless a more specific route matches a packet. Depending on the tool used and its location in a routing table, the default route may appear as default, *, or 0.0.0.0. For the purpose of this discussion, let's focus on the 0.0.0.0 implementation.
Continuing with the default motif, imagine you only want a single route in your routing table to pass all traffic. To do that, you'll need a default route that filters all traffic. When both the default route destination and netmask values are 0.0.0.0, the result is nothing will be masked. Put another way, all traffic will be diverted to that route. Since the masked address (netmask) is used as an inverse operator to create the range, this means your total range becomes 0.0.0.0 - 255.255.255.255 or everything! It's easier to understand when broken down step-by-step.
Start with the host IPv4 address. This will be the "bottom" or beginning of your address range.
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| IPv4 Host | 0.0.0.0 | 00000000.00000000.00000000.00000000 | Original host address |
Now, let's introduce the netmask. How would you capture every possible IPv4 address?
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| IPv4 Host | 0.0.0.0 | 00000000.00000000.00000000.00000000 | Original host address |
| Netmask | 0.0.0.0 | 00000000.00000000.00000000.00000000 | Network mask |
By not restricting the range at all. Essentially, by not having a mask. This is the same thing as using a route destination with slant zero (/0), or a route prefix/slant notation of 0.0.0.0/0. In practice, you would be unlikely to do this for any purpose other than the default route, because a slant notation of /0 says, "mask zero (0) bits," or in other words, "don't mask anything."
Netmask /0 = NOTHING!
Let's examine the process in more detail to clearly understand what's going on here.
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| IPv4 Host | 0.0.0.0 | 00000000.00000000.00000000.00000000 | Original host address |
| Netmask | 0.0.0.0 | 00000000.00000000.00000000.00000000 | Network mask |
| Lower Boundary | 0.0.0.0 | 00000000.00000000.00000000.00000000 | {Host Address} AND {Netmask} |
We've got the lower boundary address. Now we need the upper boundary. Finding that requires the wildcard, so let's determine that next.
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| IPv4 Host | 0.0.0.0 | 00000000.00000000.00000000.00000000 | Original host address |
| Netmask | 0.0.0.0 | 00000000.00000000.00000000.00000000 | Network mask |
| Lower Boundary | 0.0.0.0 | 00000000.00000000.00000000.00000000 | {Host Addr} AND {Netmask} |
| Wildcard | 255.255.255.255 | 11111111.11111111.11111111.11111111 | NOT {Netmask} |
Got the wildcard mask. Next up is the upper boundary calculation, which is the last IPv4 address in the range of the filter. The upper boundary is calculated by processing a logical OR between the lower boundary and wildcard mask.
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| IPv4 Host | 0.0.0.0 | 00000000.00000000.00000000.00000000 | Original host address |
| Netmask | 0.0.0.0 | 00000000.00000000.00000000.00000000 | Network mask |
| Lower Boundary | 0.0.0.0 | 00000000.00000000.00000000.00000000 | {Host Addr} AND {Netmask} |
| Wildcard | 255.255.255.255 | 11111111.11111111.11111111.11111111 | NOT {Netmask} |
| Upper Boundary | 255.255.255.255 | 11111111.11111111.11111111.11111111 | {Lower Boundary} OR {Wildcard} |
So, there you have it. This explains how and why a host address of 0.0.0.0 and netmask of 0.0.0.0 yields a default route or "all addresses."
Example 2: Sub my Net
Let's take a common example using some private network addresses. Your goal is to carve out a sub-net with 64 host addresses. Presume you are creating a route with IPv4 host 192.168.1.1 and netmask 255.255.255.192 (alternatively expressed using slant notation as 192.168.1.1/26). The routing calculations would look like this:
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| IPv4 Host | 192.168.1.1 | 11000000.10101000.00000001.00000001 | Original host address |
| Netmask | 255.255.255.192 | 11111111.11111111.11111111.11000000 | Network mask |
| Lower Boundary | 192.168.1.0 | 11000000.10101000.00000001.00000000 | {Host Addr} AND {Netmask} |
| Wildcard | 0.0.0.63 | 00000000.00000000.00000000.00111111 | NOT {Netmask} |
| Upper Boundary | 11000000.10101000.00000001.00111111 | {Lower Boundary} OR {Wildcard} | |
| # of hosts | 63 + 1 = 64 | n/a | Wildcard value + 1 |
Dissecting the chart above, notice the binary netmask has 26 bits flipped to 1 - thus it could alternatively be represented with slash notation as /26. And the remaining number of bits (6) matches the set bits of the wildcard.
| Value | Slash Notation | Binary | Comment |
|---|---|---|---|
| netmask | /26 | 11111111.11111111.11111111.11000000 | Network mask |
Let's break down the example above and examine how the IPv4 addressable range of the route is determined. We are looking at a destination IPv4 address of 192.168.1.1 with a netmask of 255.255.255.192 or slant notation of /26:
11111111.11111111.11111111.11 000000
The slant notation is often the easiest method of visualizing what's going on. In this example, using a slant notation of /26, we can see the first 26 bits are represented in the netmask with their bits flipped to 1:
/26 = 11111111.11111111.11111111.11 prefixed netmask
Slant notation is just another way of declaring the netmask. The purpose of the netmask is to establish the lower boundary IPv4 host address for the current route, which is obtained by masking (or excluding) its portion of the routing prefix (IPv4 host address). Since the slant notation masks the prefix, only the bits to the right of the prefix are used in determining the lower boundary of the route's range. In the example above there are 26-bits used in the netmask. Since there are always 32-bits total in the IPv4 host address, this leaves 6-bits (32 - 26 = 6) remaining that will not be preserved by the netmask. That means those six (6) bits will be evaluated by the process that determines the lower boundary IPv4 address, thus beginning to define the range of addresses in the route.
Bear in mind the lower boundary might might not be equal to the starting IPv4 host address. Take a look at the current example:
192.168.1.1 = 11000000.10101000.00000001.00000001
Let's carve out the trailing 6-bits of the host address not protected by the netmask (remember, only the first 26-bits are masked in this example).
192.168.1.1 = 11000000.10101000.00000001.00 000001
Note the last digit of the host address is a 1.
192.168.1.1 = 11000000.10101000.00000001.00 000001
Applying the required AND logic operation to the original host address and netmask, the lower end of the range after the netmask (in this case, after the 26th bit) is forcibly zeroed out by the trailing end of the netmask.
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| IPv4 Host | 192.168.1.1 | 11000000.10101000.00000001.00000001 | Host address |
| AND | |||
| Netmask | 255.255.255.192 | 11111111.11111111.11111111.11000000 | Network mask |
Yields:
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| Lower Boundary | 192.168.1.0 | 11000000.10101000.00000001.00000000 | {Host Addr} AND {Netmask} |
As you can see, the starting point of the network segment has been forced lower (to 192.168.1.0) than the original starting position (192.168.1.1). It's probably not a big deal in this particular case, but it does highlight the fact the original host address will not necessarily be the lower boundary for any given route.
Now let us turn our attention to the next level in the example: the wildcard.
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| Wildcard | 0.0.0.63 | 00000000.00000000.00000000.00111111 | NOT {Netmask} |
The wildcard mask also has 26 bits (but they are flipped to 0 - the opposite result of the netmask). By isolating the bits exclusive of the prefix, the wildcard mask determines the size of the range. The value of those remaining bits becomes the range of IPv4 host addresses encompassed by the route and is used to determine the IPv4 host address upper boundary applicable to the route.
The wildcard mask is the opposite of the netmask. Turning our attention to the current example,....
11111111.11111111.11111111.11 000000 [net-mask]
00000000.00000000.00000000.00 111111 [wildcard]
The purpose of the wildcard mask is to expose the size or range of host addresses applicable to the route. It is the last portion of the bits - the ones excluded from the netmask - that you want to pay attention to. So, in this example, the last 6 bits of the 32-bit string are the only bits that will be applied as part of the "range" for this particular route. The lower boundary of the address range is established by a combination of host address and netmask. Let's take a closer look at this example:
11111111.11111111.11111111.11 000000
Translates to 192.168.1.0
While the wildcard bits after the mask indicate the range or size of the network, which in this case is the number of IPv4 host addresses:
00000000.00000000.00000000.00 111111
You can now add the size or range of addresses to the starting address and find the upper boundary host address:
Which translates to 192.168.1.63
As you can see, we have a total range for this route of 192.168.1.0 - 192.168.1.63. Notice the number of IP addresses in the range (64) is equal to the wildcard mask (111111). Recall the wildcard mask:
00000000.00000000.00000000.00 111111
Extracting the bits after the netmask slant (26 bits), we get 6 bits remaining. That number (111111) represents 64 in the 10-base numbering system. And as you can see, the range is indeed 64 host addresses, inclusive. Mission accomplished!
Example 3: 255 is the Opposite of 0 (Zero) [a.k.a. Singling Out Single Hosts]
One of the more common routing tasks is directing a route to a specific host. Thankfully, it's a simple task to implement in a routing table. In fact, I would say the process represents the most basic route possible in a routing table. Targetting a single IPv4 host address is the exact opposite of creating a default route.
Hopefully, by now you've already ascertained the number 255 has special meaning in netmasks. When all bits of an IPv4 address byte are set to one (1), the 8-bit value is 255. In the context of a netmask, this translates to, "Restrict the range to only the number presented in the corresponding octet of the destination address." How? Each of those octets is a number from 0 to 255. When the mask is set to 255, it allows all the bits to match and pass through. Take a look at this visual representation of a mask that is 255.255.255.255.
Let's take a common example using some private network addresses. Your goal is to carve out a sub-net of one (1) host address. Presume you are creating a route with IPv4 host 192.168.1.1 and netmask 255.255.255.255 (alternatively expressed using slant notation as 192.168.1.1/32). The routing calculations would look like this:
| Value | 10-base | Binary | Comment |
|---|---|---|---|
| IPv4 Host | 192.168.1.1 | 11000000.10101000.00000001.00000001 | Original host address |
| Netmask | 255.255.255.255 | 11111111.11111111.11111111.11111111 | Network mask |
| Lower Boundary | 192.168.1.1 | 11000000.10101000.00000001.00000001 | {Host Addr} AND {Netmask} |
| Wildcard | 0.0.0.0 | 00000000.00000000.00000000.00000000 | NOT {Netmask} |
| Upper Boundary | 11000000.10101000.00000001.00000001 | {Lower Boundary} OR {Wildcard} | |
| # of hosts | 0 + 1 = 1 | n/a | Wildcard value + 1 |
Notice what happens to the host address when it is masked by the netmask. All the bits of the host address are masked, meaning they are preserved and fall through to the other side. The net result is a route of one (1) IPv4 address.
Suggested IPv4 Netmask Calculation Tools
An informal list of suggested tools for netmask and CIDR calculations.
| ipcalc | Linux terminal | Found in most distros |
|---|---|---|
| Netmask Quick Reference Chart | Web | Steve Friedl's Netmask Quick Reference Guide |
| CIDR calculator | Web | CIDR/VLSM supernet calculator |
| CIDR to IPv4 Conversion | Web | IPLocationTools |
Footnotes
1 The term "DNS" may be used to represent either of two (2) distinct, but related concepts. DNS can refer to a Domain Name System or Domain Name Server. The latter is simply a server operating or part of the operation of the former.

